Using PyEDA to Solve Sudoku¶
According to Peter Norvig in his fantastic essay on solving every Sudoku puzzle using Python, security expert Ben Laurie once stated that “Sudoku is a denial of service attack on human intellect”. I can personally attest to that.
In this example, I will explain how to use PyEDA’s Boolean expressions and satisfiability engine to create a general-purpose Sudoku solver.
First, let’s get a few ground rules straight:
- There are lots of Sudoku solvers on the Internet; I make no claims of novelty.
- PyEDA is pretty fast, but unlikely to win any speed competitions.
- Let’s face it–this is a pretty awesome waste of time.
Getting Started¶
First, import all the standard symbols from PyEDA.
>>> from pyeda.inter import *
Let’s also define a variable “DIGITS” that makes it easier to access the Sudoku square values.
>>> DIGITS = "123456789"
Setting Up the Puzzle Grid¶
A Sudoko puzzle is a 9x9 grid. Each square in the grid may contain any number in the digits 1-9. The following example grid was generated by Web Sudoku.
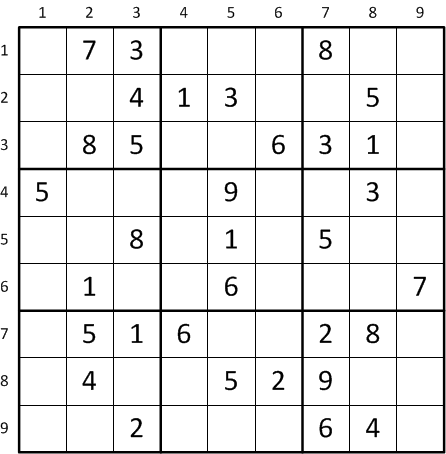
Example Sudoku Grid
To represent the state of the grid coordinate, create a 3-dimensional variable, X.
>>> X = exprvars('x', (1, 10), (1, 10), (1, 10))
exprvars is a versatile function for returning arrays of arbitrary dimension. The first argument is the variable name. Each additional argument adds an additional dimension with a non-negative start and stop index. If you provide only a number instead of a two-tuple, the start index is zero. For example, we could also have used exprvars('x', 9, 9, 9), but that would have given X[0:9, 0:9, 0:9] instead of X[1:10, 1:10, 1:10].
The variable X is a 9x9x9 bit vector, indexed as X[row, column, value]. So for the Example Sudoku Grid, since row 5, column 3 has value ‘8’, we would represent this by setting X[5,3,8] = 1.
Constraints¶
Now that we have a variable X[r,c,v] to represent the state of the Sudoku board, we need to program the constraints. We will use the familiar Boolean And function, and the OneHot function. In case you are not familiar with the OneHot function, we will describe it here.
One Hot Function¶
Let’s say I have three variables, a, b, and c.
>>> a, b, c = map(exprvar, 'abc')
I want to write a Boolean formula that guarantees that only one of them is true at any given moment.
>>> f = OneHot(a, b, c)
You can use PyEDA to automatically produce the truth table.
>>> expr2truthtable(f)
inputs: c b a
000 0
001 1
010 1
011 0
100 1
101 0
110 0
111 0
By default, the OneHot function returns a formula in conjunctive normal (product-of-sums) form. Roughly translated, this formula says that “no two variables can both be true, and at least one must be true”.
>>> f
And(Or(~a, ~b), Or(~a, ~c), Or(~b, ~c), Or(a, b, c))
In disjunctive normal (sum-of-products) form, the function looks like this:
>>> f.to_dnf()
Or(And(~a, ~b, c), And(~a, b, ~c), And(a, ~b, ~c))
Value Constraints¶
You probably already noticed that if the square at (5, 3) has value ‘8’, it is not allowed to have any other value. That is, if X[5,3,8] = 1, then X[5,3,1:10] == [0, 0, 0, 0, 0, 0, 0, 1, 0].
We need to write a constraint formula that says “every square on the board can assume only one value.” With PyEDA, you can write this formula as follows:
>>> V = And(*[
... And(*[
... OneHot(*[ X[r, c, v]
... for v in range(1, 10) ])
... for c in range(1, 10) ])
... for r in range(1, 10) ])
Row and Column Constraints¶
Next, we need to write formulas that say “every square in each row is unique”, and “every square in each column is unique”, respectively.
>>> R = And(*[
... And(*[
... OneHot(*[ X[r, c, v]
... for c in range(1, 10) ])
... for v in range(1, 10) ])
... for r in range(1, 10) ])
>>> C = And(*[
... And(*[
... OneHot(*[ X[r, c, v]
... for r in range(1, 10) ])
... for v in range(1, 10) ])
... for c in range(1, 10) ])
Box Constraints¶
The box constraints are a little tricker. We need a formula that says “every square in a box is unique”. The key to understanding how to write this formula is to think of the grid as consisting of 3x3 boxes. Now instead of iterating over the nine squares in a row or column, we will iterate over the 3 rows and 3 columns of the 3x3 boxes.
>>> B = And(*[
... And(*[
... OneHot(*[ X[3*br+r, 3*bc+c, v]
... for r in range(1, 4) for c in range(1, 4) ])
... for v in range(1, 10) ])
... for br in range(3) for bc in range(3) ])
Putting It All Together¶
Now that we have the value, row, column, and box constraints, we need to combine them all into a single formula. We will use the And function to join the constraints, because all constraints must be true for the puzzle to be solved.
>>> S = And(V, R, C, B)
>>> len(S.args)
10530
As you can see, the constraints formula is quite large.
Preparing the Input¶
We now have the generic constraints for the rules of Sudoku, but when you sit down to solve a puzzle, you are always given a set of known values. These are the inputs, and they will further constrain the solution.
Here is a function to parse an input string, and produce the input constraints. Any character in the set 1-9 will be taken as an assignment, the values ‘0’ and ‘.’ (period) will be taken as an unknown, and all other characters will be ignored. This function also returns a CNF data type.
>>> def parse_grid(grid):
... chars = [c for c in grid if c in DIGITS or c in "0."]
... assert len(chars) == 9 ** 2
... return And(*[ X[i // 9 + 1, i % 9 + 1, int(c)]
... for i, c in enumerate(chars) if c in DIGITS ])
The example grid above can be written like this:
>>> grid = ( ".73|...|8.."
... "..4|13.|.5."
... ".85|..6|31."
... "---+---+---"
... "5..|.9.|.3."
... "..8|.1.|5.."
... ".1.|.6.|..7"
... "---+---+---"
... ".51|6..|28."
... ".4.|.52|9.."
... "..2|...|64." )
Display Methods¶
To display the solution, we will need some methods. The PyEDA SAT solver returns a dictionary that represents a “point” in an N-dimensional Boolean space. That is, it maps N Boolean variables (in our case 729) onto their values in {0, 1}.
>>> def get_val(point, r, c):
... for v in range(1, 10):
... if point[X[r, c, v]]:
... return DIGITS[v-1]
... return "X"
>>> def display(point):
... chars = list()
... for r in range(1, 10):
... for c in range(1, 10):
... if c in (4, 7):
... chars.append("|")
... chars.append(get_val(point, r, c))
... if r != 9:
... chars.append("\n")
... if r in (3, 6):
... chars.append("---+---+---\n")
... print("".join(chars))
Finding the Solution¶
Without further ado, let’s use the PicoSAT fast SAT solver to crunch the numbers.
>>> def solve(grid):
... with parse_grid(grid):
... return S.satisfy_one()
Here is the solution to the Example Sudoku Grid:
>>> display(solve(grid))
173|529|864
694|138|752
285|476|319
---+---+---
567|294|138
428|713|596
319|865|427
---+---+---
951|647|283
846|352|971
732|981|645
That example was actually a pretty easy puzzle. Let’s see how the Sudoku solver handles a few harder puzzles.
>>> grid = ( "6..|3.2|..."
... ".5.|...|.1."
... "...|...|..."
... "---+---+---"
... "7.2|6..|..."
... "...|...|.54"
... "3..|...|..."
... "---+---+---"
... ".8.|15.|..."
... "...|.4.|2.."
... "...|...|7.." )
>>> display(solve(grid))
614|382|579
953|764|812
827|591|436
---+---+---
742|635|198
168|279|354
395|418|627
---+---+---
286|157|943
579|843|261
431|926|785
>>> grid = ( "38.|6..|..."
... "..9|...|..."
... ".2.|.3.|51."
... "---+---+---"
... "...|..5|..."
... ".3.|.1.|.6."
... "...|4..|..."
... "---+---+---"
... ".17|.5.|.8."
... "...|...|9.."
... "...|..7|.32" )
>>> display(solve(grid))
385|621|497
179|584|326
426|739|518
---+---+---
762|395|841
534|812|769
891|476|253
---+---+---
917|253|684
243|168|975
658|947|132